自己动手画 CPU《计算机组织与结构实验》（二）

# cpu, 2020-10-04

• 二、运算器组成实验
  • 1. 可控加减法电路设计实验
  • 2. 4 位先行进位74182
  • 3. 4 位快速加法器设计
  • 4. 16 位快速加法器设计
  • 5. 32 位快速加法器设计
  • 6. 32 位 ALU设计实验
  • 7. 5 位阵列乘法器
    • 1）前置背景
    • 2）横向进位阵列乘法器
    • 3）斜向进位阵列乘法器
  • 8. 6 位补码阵列乘法器
  • 9. 5 位无符号乘法流水线
  • 10.原码 1 位乘法器设计实验
  • 11.补码 1 位乘法器设计实验

配套慕课

二、运算器组成实验

1. 可控加减法电路设计实验

1、背景知识

0）一位加法逻辑电路实现

• 0＋1=1 1＋0=1
• 1＋1=0 0＋0=0
• 因此：一个异或门即可实现 自动 一位加法

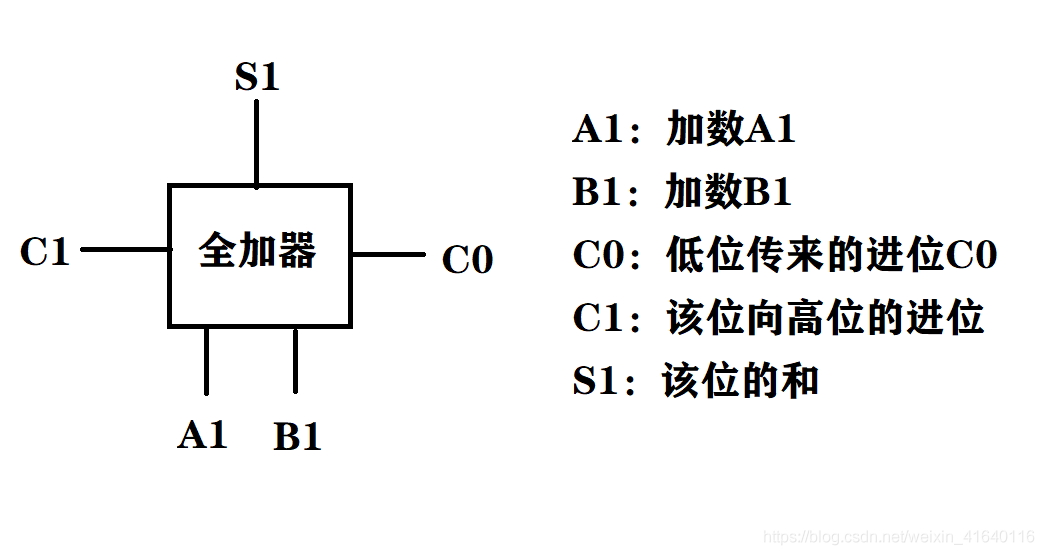
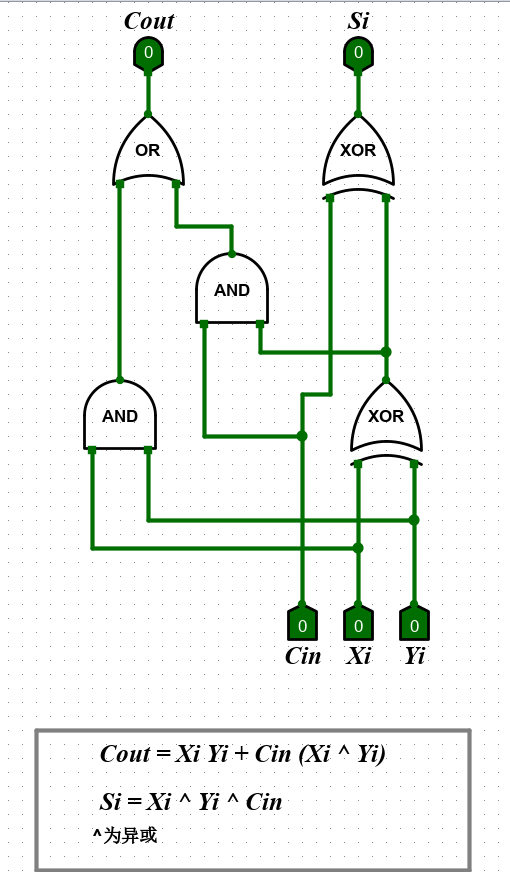
1）一位全加器的实现。

一位全加器的表达式如下：

1. Si = Xi ⊕ Yi ⊕ Cin

2. Cout = XiYi + （Xi ⊕ Yi）Cin

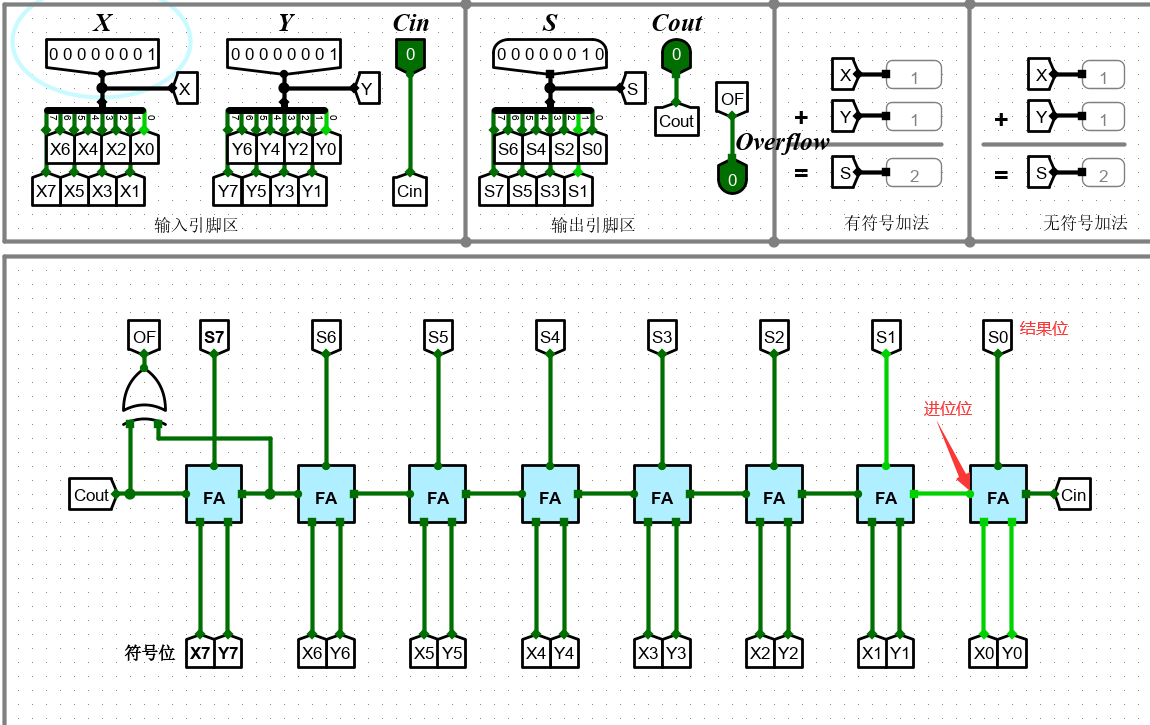
2）多位串行加法器

判断溢出方式为：

1. 无符号数溢出判断：其实很简单，就一句话：

   当最高为向更高位有进位（或借位）时产生溢出

由于无符号数通常代表内存地址，这种情况下的溢出可以忽略。

1. 溢出只可能符号数溢出的情况，包括[X]补与[Y]补，[X]补与[-Y]补同号。

   方法一：对操作数和运算结果的符号位进行检测，如果不相同则发生了溢出。

   设X0，Y0为运算数的符号位，S0为运算结果的符号位。

   逻辑表达式为：OF = X0Y0~S0 + ~X0~Y0S0

   当OF = 1时发生溢出。

   方法二：对最高数据位进位和符号位进位进行检测。

   设最高数据位产生的进位为C1，符号位产生的进位为C0.

   两个正数相加，此时C0 = 0，若C1 = 1，则改变了结果符号位。发生溢出。

   两个负数相加，此时C0 = 1， 若C1 = 0，则改变了结果符号位。发生溢出。

   逻辑表达式为：OF = C0⊕C1

   方法三：使用变形补码，给数据加上两位符号位，正常情况，符号位应该相同，如果运算后的结果两位符号位不同，则发生溢出。

电路图中的第一位全加器的低位进位默认是没有进位的，只有输入位。

本实验采用方法二，对于 最高数据位进位 和 符号位进位 两个位数进行异或检测

3）8位可控加减法器

原理：

[X]补 - [Y]补 = [X - Y]补 = [X]补 + [-Y]补

[-Y]补 = [[Y]补]补

进行减法时，根据减法运算，需要把 [Y]补 转换为 [-Y]补 。转换规则与原码转补码相同，所以直接取反加一即可。

eg：[Y]补 = 10011 [-Y]补 = 01101

设计思路：加上一个 Sub 控制信号输入，输入数 Y 的所有位 Yi 均与 Sub 位进行异或后送入 全加器 中。

• 当 Sub = 0 时，送入为 Y 本身；
• 当 Sub = 1 时，送入为 Y 的反码；且 Sub 位也连在加法器上，因此 Sub 为 1 时，直接取反码后再加上 1，而 Sub 为 0 时，进位 0 不影响加法结果

最终实现如下

此时 Sub 位 为 0 ，表示加法（下侧运算指示由 LED 点阵表示）

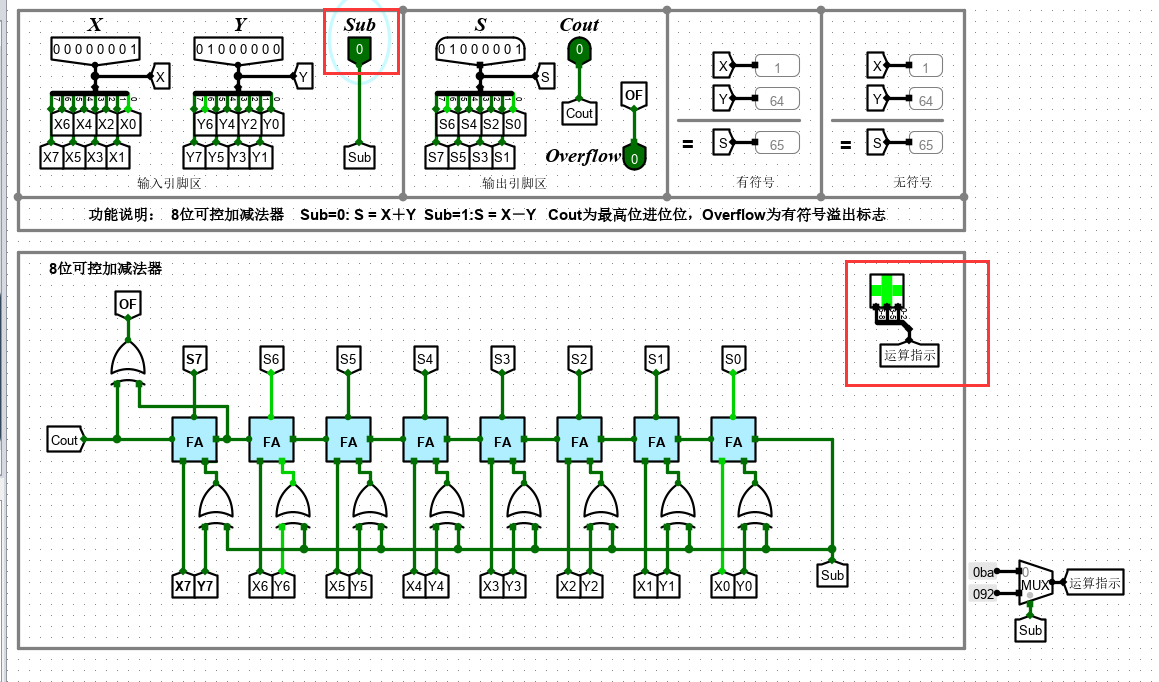
此时 Sub 位 为 1 ，表示减法

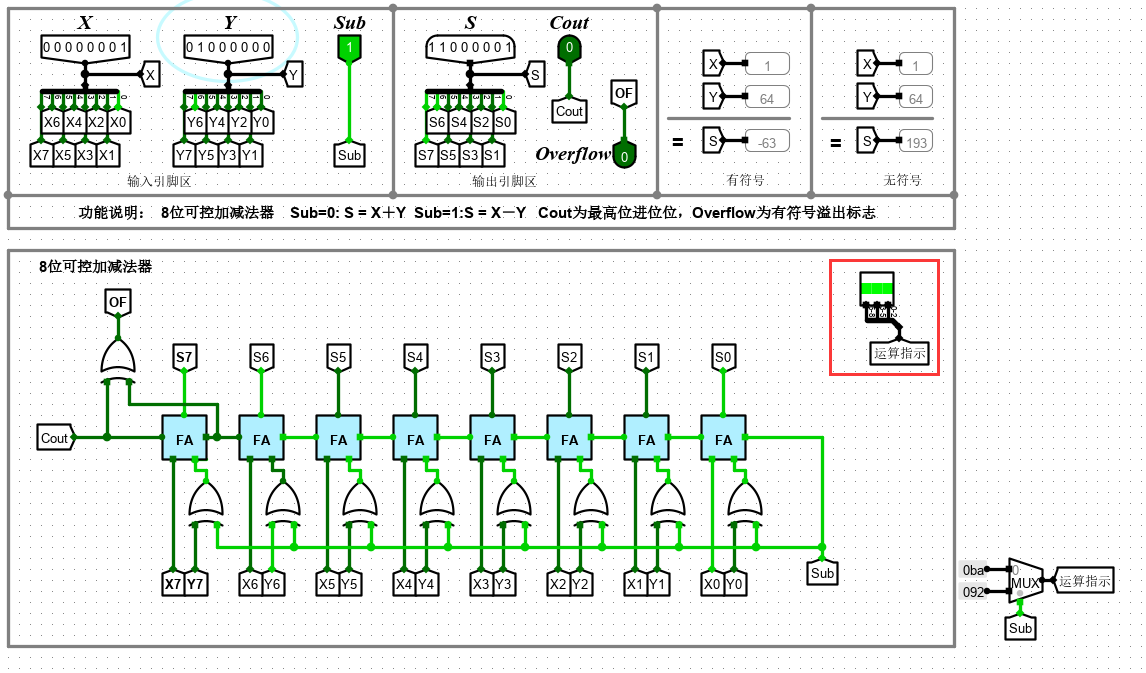
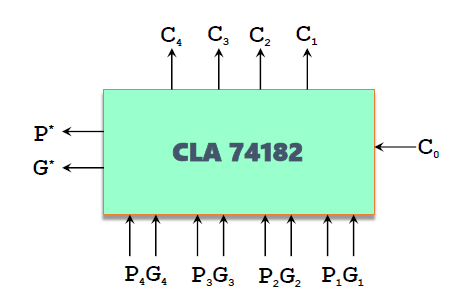
2. 4 位先行进位74182

由于全加器公式如下，即高位运算取决于低位运算的输入 Ci-1。因此不能进行并行运算

1. Si = Xi ⊕ Yi ⊕ Cin
2. Cout = XiYi + （Xi ⊕ Yi）Cin / Cout = XiYi + （Xi + Yi）Cin

即如上图可知，一般采用 4 位一组的先行进位方法。

设 进位生成函数 Gi = XiYi， Pi = Xi ⊕ Yi

由上图我们可以提取出以下公式

Ci = Gi + Pi*Ci-1

则

C1 = G1 + P1*C0

C2 = G2 + P2*C1

C3 = G3 + P3*C2

C4 = G4 + P4*C3

逐步带入可得

C2 = G2 + P2*（ G1 + P1 * C0）

= G2 + P2G1 + P2P1C0

C3 = G3 + P3 *（G2 + P2G1 + P2P1C0）

= G3 + P3G2 + P3P2G1 + P3P2P1C0

C4 = G4 + P4*（G3 + P3G2 + P3P2G1 + P3P2P1C0）

= G4 + P4G3 + P4P3G2 + P4P3P2G1 + P4P3P2P1C0

这里可以发现各级的进位与其他进位无关

而 所有的 P、G输入后需要 2T 的时间延迟；

又因为P、G输入需要一级门电路延迟，因此总输入为 3T 延迟。

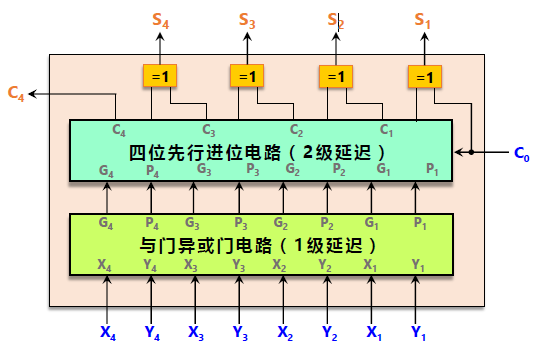
构造电路图如下

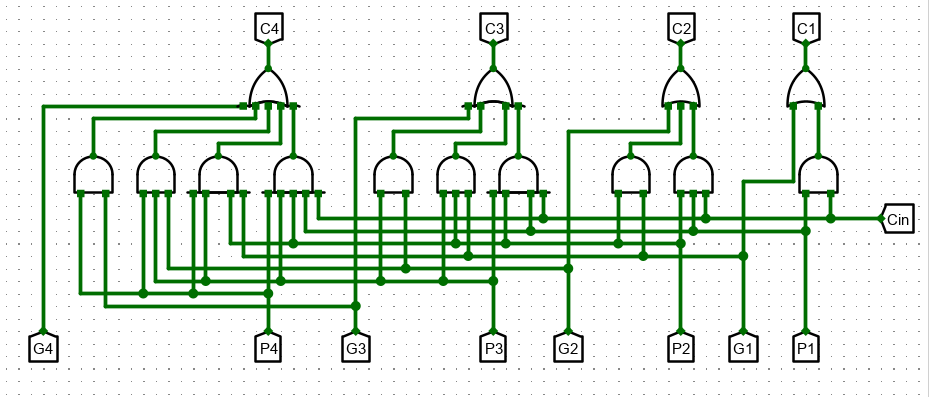
现在已经得到 4 位的加速加法器，若想得到更多位宽电路，如 16 位加法器，最简单的方法便是将 4 个加法器进位链 进行串联，但是这样的话只能实现 4 位组内并行计算，组间还是串行。

因此现在希望提高性能：

成组进位生成函数：G* = G4 + P4G3 + P4P3G2 + P4P3P2G1

成组进位传递函数：P* = P4P3P2P1

我们发现：C4 = G4 + P4G3 + P4P3G2 + P4P3P2G1 + P4P3P2P1C0 = G* + P* C0

即与之前提到的先行进位中的 C1 = G1 + P1*C0 形式完全一样！即只要提前得到 成组进位生成函数 和 成组进位传递函数，再复用 4 位先行进位电路即可。

生成电路如下：

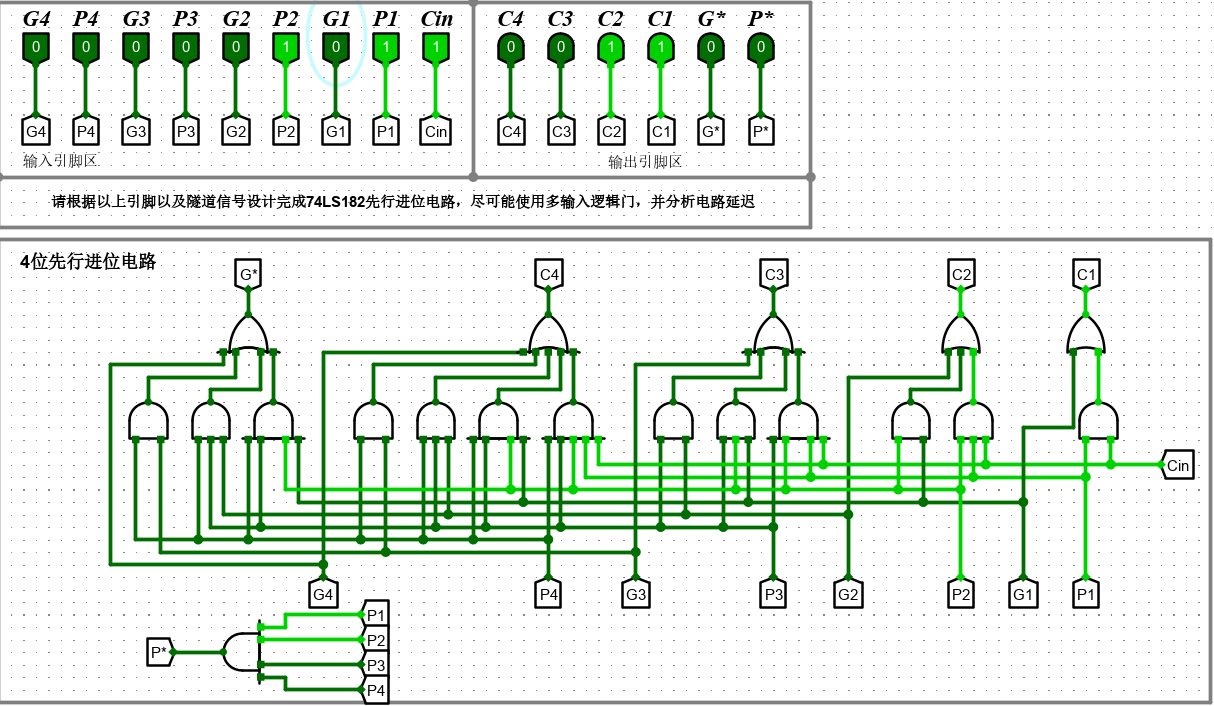
3. 4 位快速加法器设计

按照下图 74182 4 位加法器

通过此处的与门异或门电路得到相应输入值，再输入即可

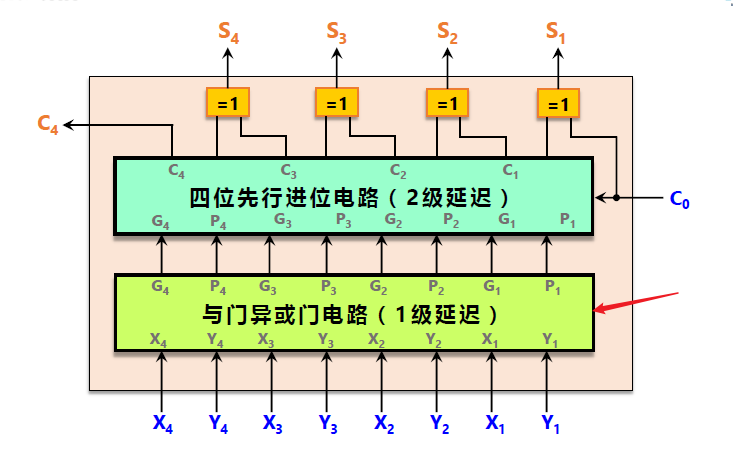
实现电路如下

注意 ：C3 只是一个输出位。

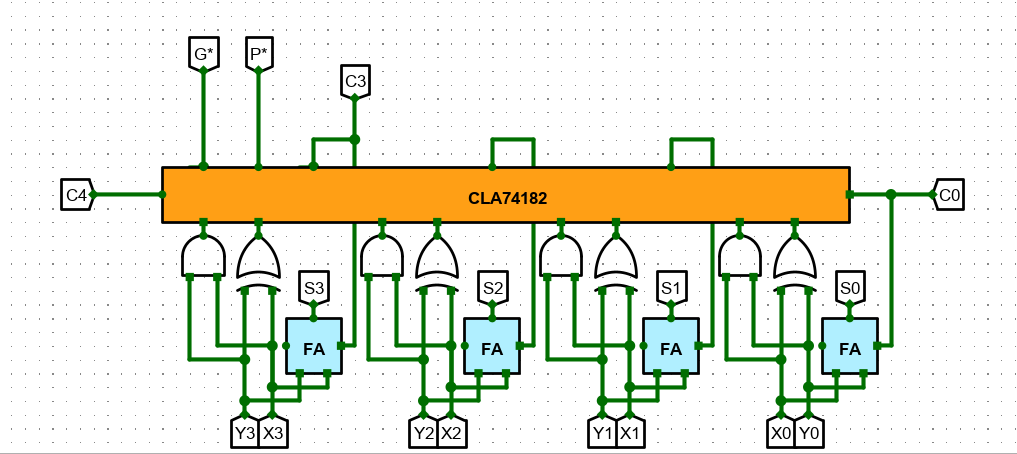
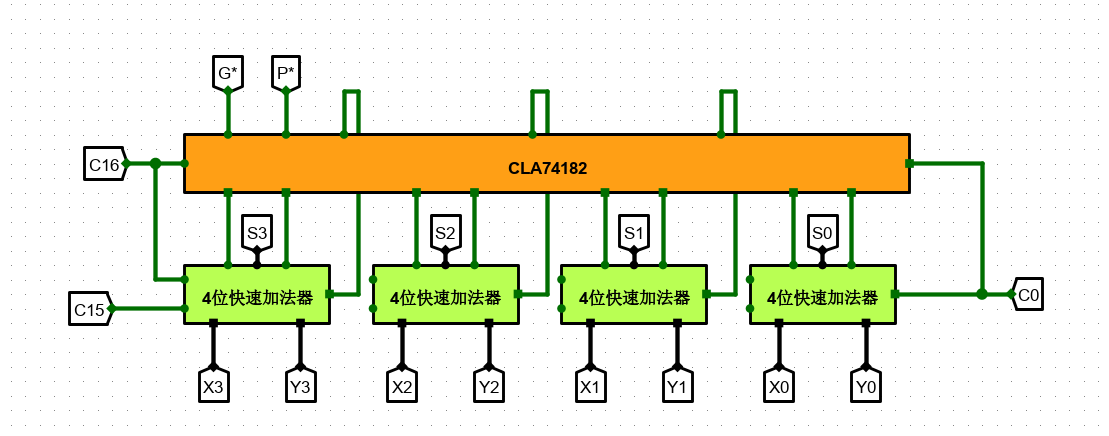
4. 16 位快速加法器设计

主要思想便为：组内并行，组间并行。

设计思路较为简单，由上层 CLA74182 产生下层所需要的 C4、C8、C12，再并行运算得到各个进位，再输回4位快速加法器,得到 Cout 。

具体步骤是：底层加速加法器首先生成所有 P，G（时间延迟为 1T），接着产生 P*、G*（即输入进CLA的电路端，时间延迟为 2T），上层先行电路 CLA 通过 P、G、C0得到 C4、C8、C12 信号（时间延迟为 2T），此时下层加法器的所有输入信号都已经待续，经过内部的 C0 与其他信号的与门异或门（2T) 以及 S 的求和运算（P 与 C的异或，时间延迟为 1T），因此最终延迟为 8T。

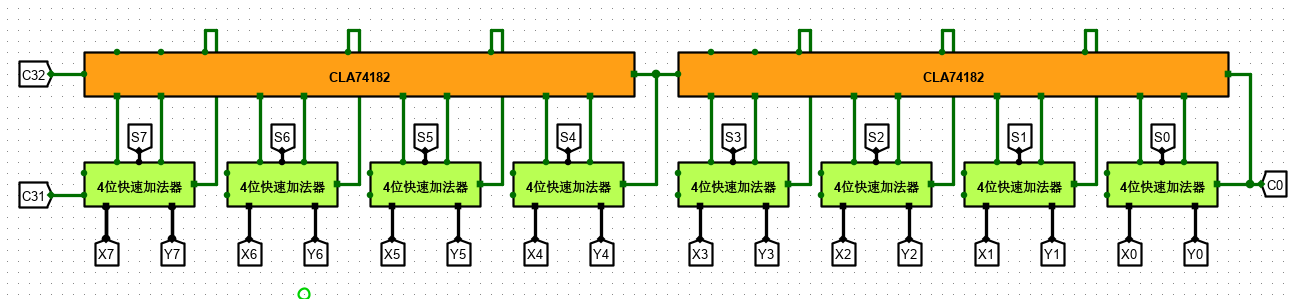
5. 32 位快速加法器设计

思路与上面大致一样，不再赘述。

6. 32 位 ALU设计实验

【目标】

​利用前面实验封装好的32位加法器以及 Logisim 平台中现有运算部件，构建一个32位算术逻辑运算单元（禁用 Logisim 系统自带的加法器，减法器），可支持算术加、减、乘、除，逻辑与、或、非、异或运算、逻辑左移、逻辑右移、算术右移运算，支持常用程序状态标志（有符号溢出 OF 、无符号溢出 UOF ，结果相等 Equal ），ALU 功能以及输入输出引脚见下图。

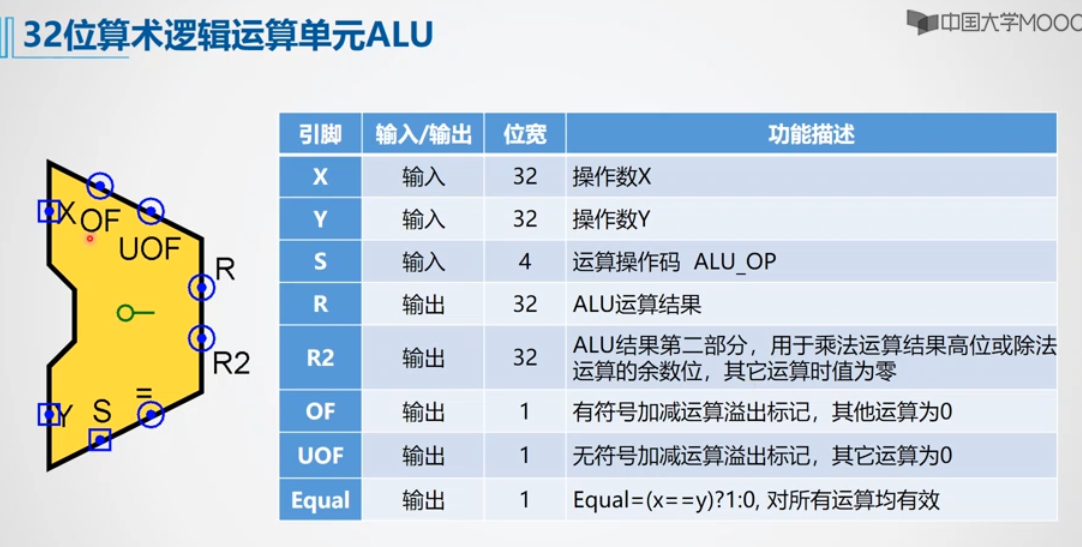
ALU 功能

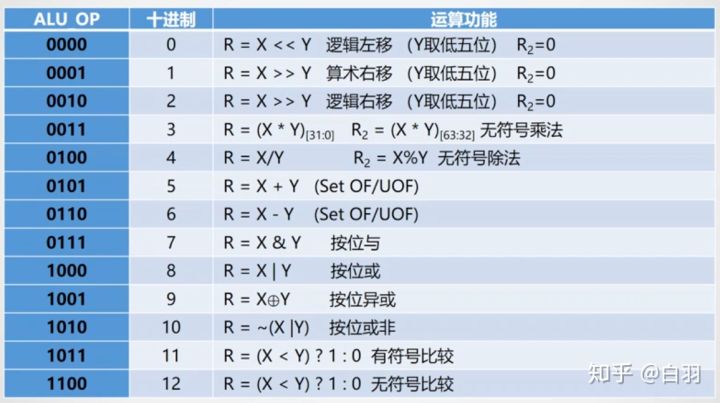
实现电路如下：

主要注意以下几处：

1. 移位器采用分线器来得到 Y 的低五位
2. 减法的运用 32 位加法器时，需直接判断 X 是否 无符号大于 Y 即可。
3. 再就是 比较器 的设置！！！

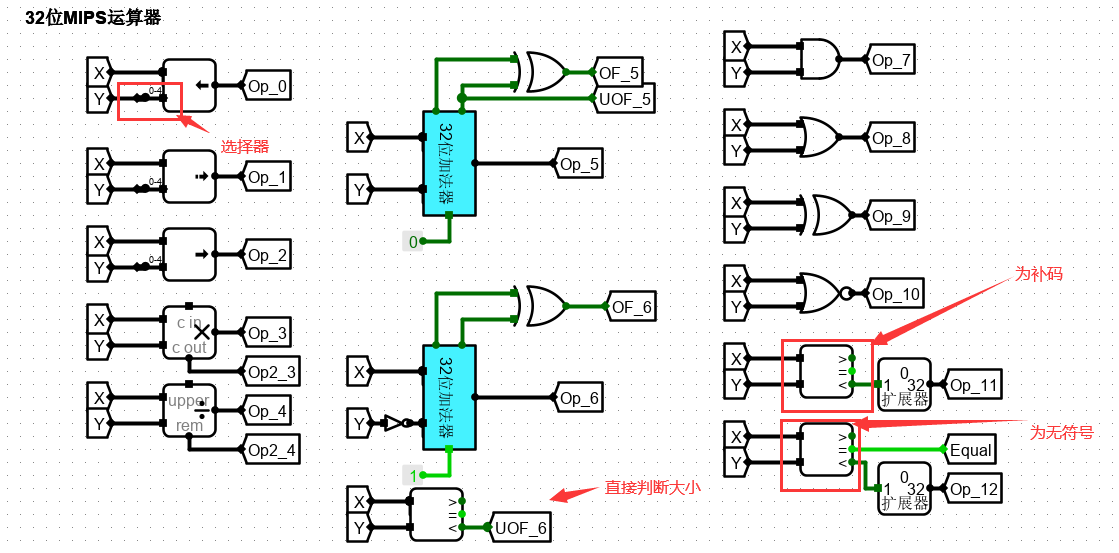
选择器的运用

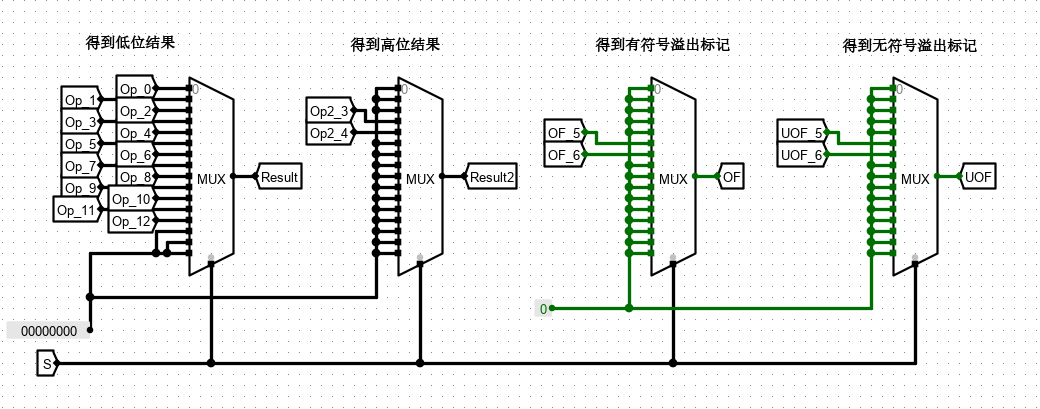
折磨我一个小时的问题！！！！

比较器无符号的比较！！！

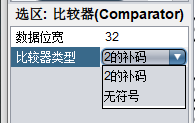
最终测试结果

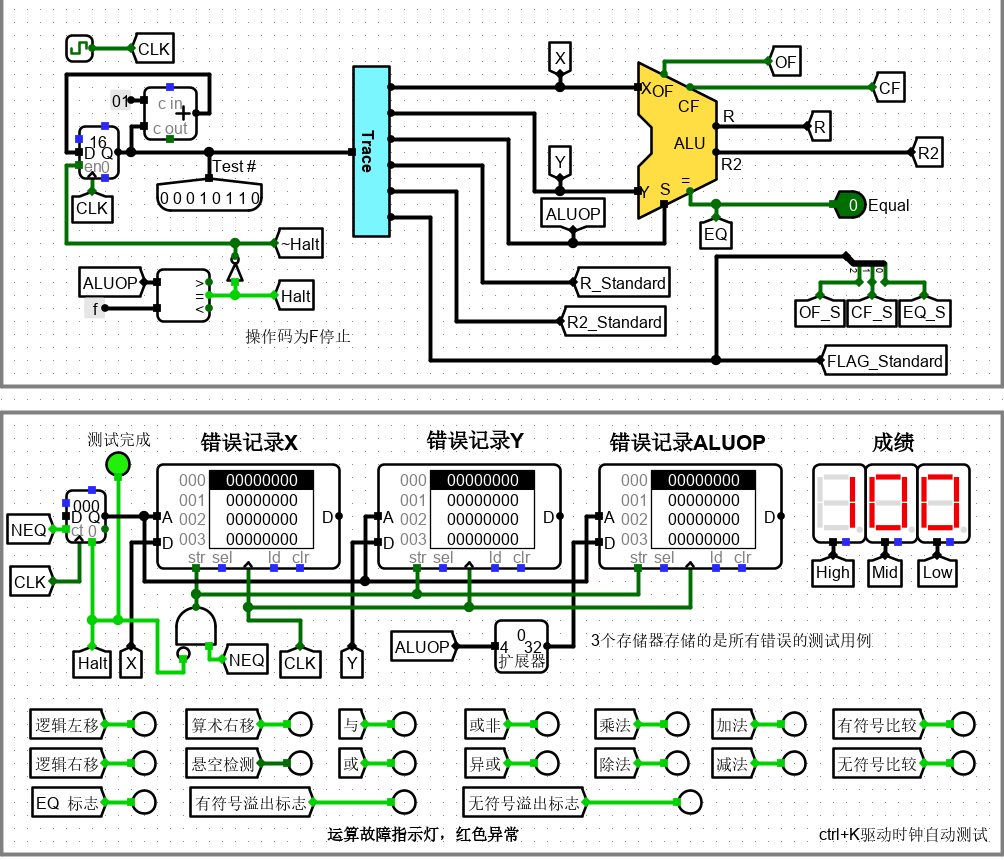
7. 5 位阵列乘法器

1）前置背景

乘法实现类似于现实生活中的乘法方法(如下图)

而相加数的得到需要考虑一位乘法的实现：

1×1=1
1×0=0
0×1=0
0x0=0

即类似与门

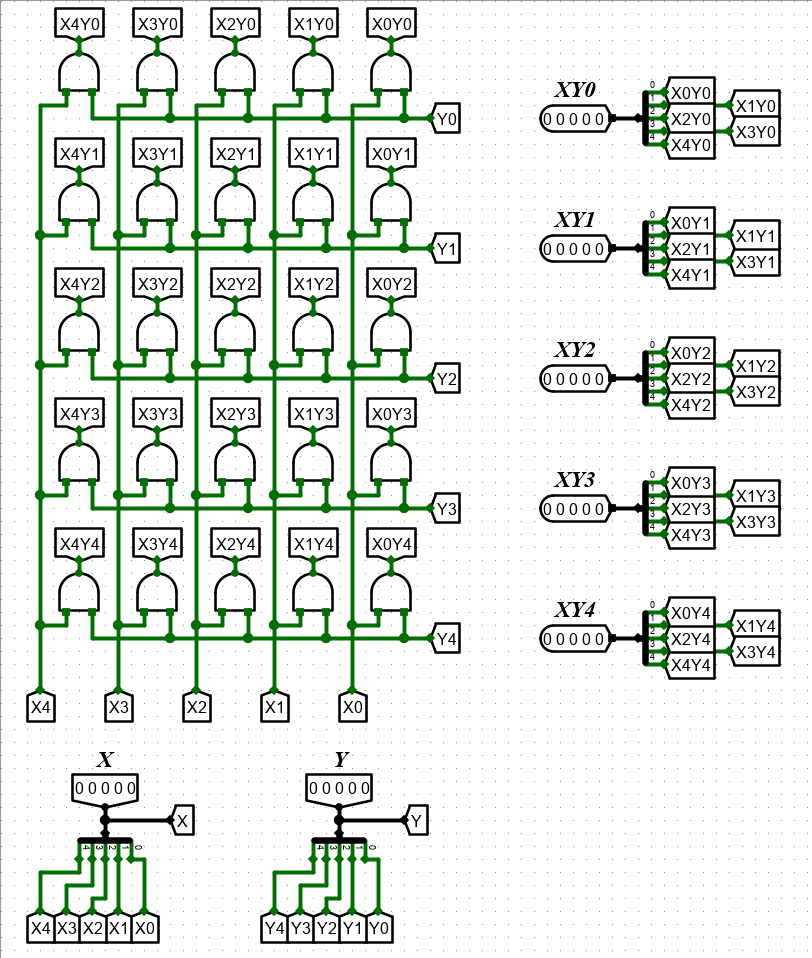
由上图与门得到相加数，采用 25 个与门并发产生。————一级门延迟

2）横向进位阵列乘法器

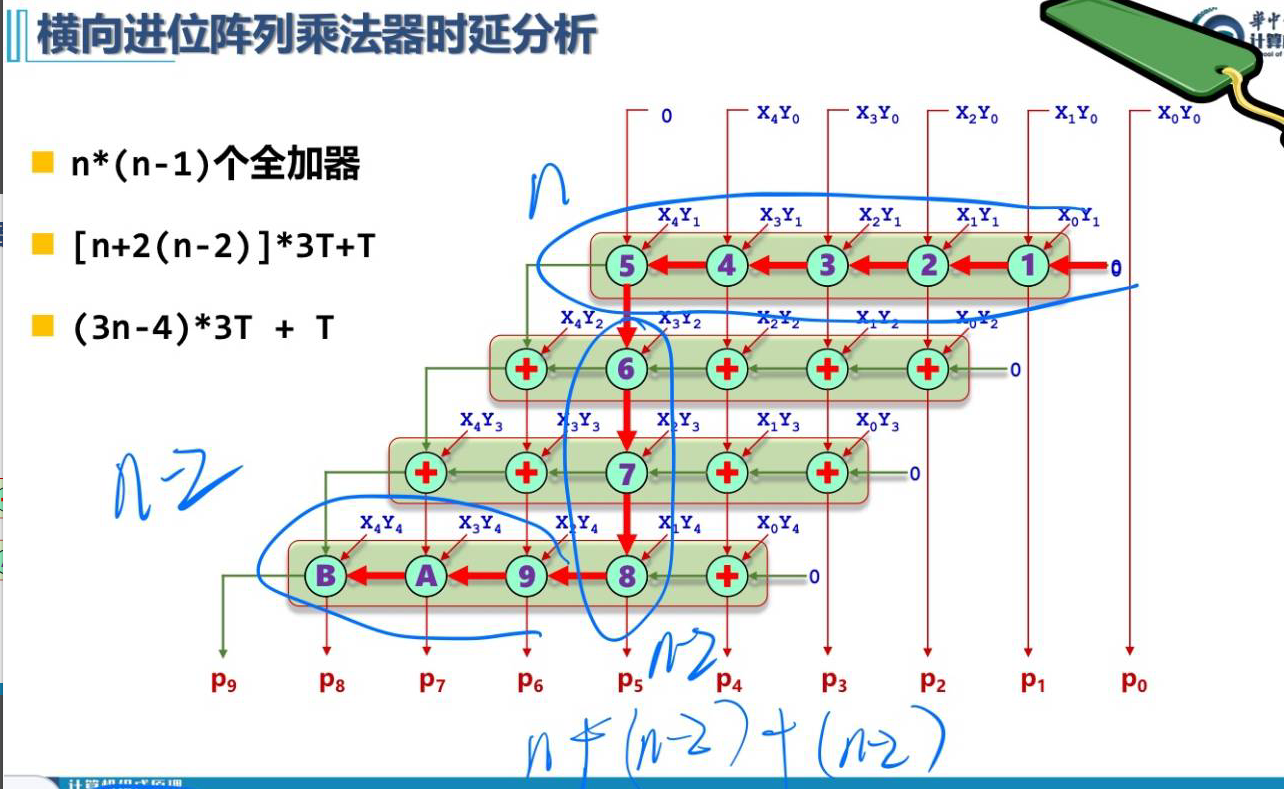
易知延迟如上图（+T 表示与门的延迟时间）

实现电路如下

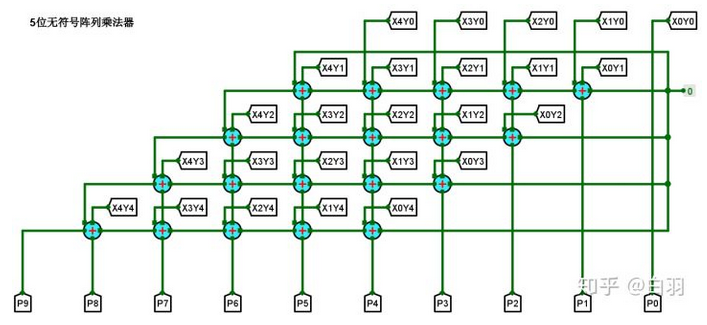
其中加法器的各个接口如下：

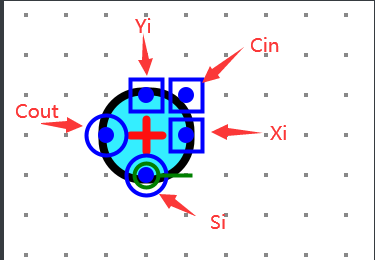
3）斜向进位阵列乘法器

我们发现横向进位加法器过于依赖进位，若改为斜向进位，那么只有最后一行需要依赖横向进位，能较好的提升乘法器性能。

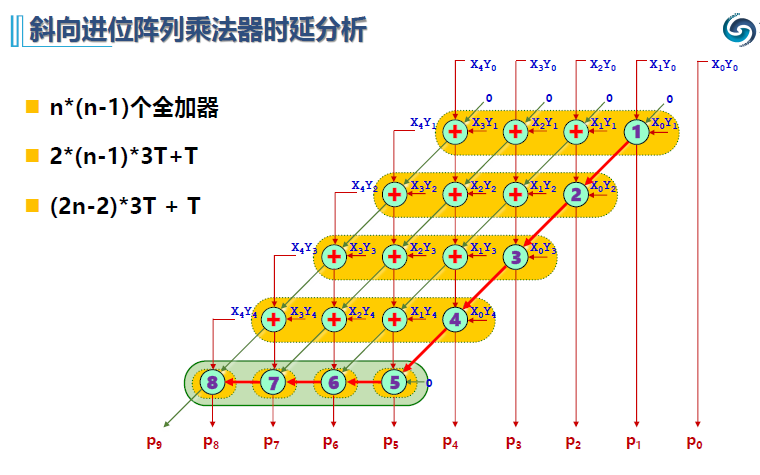
易知延迟如上图（+T 表示与门的延迟时间）

最终电路实现如下：

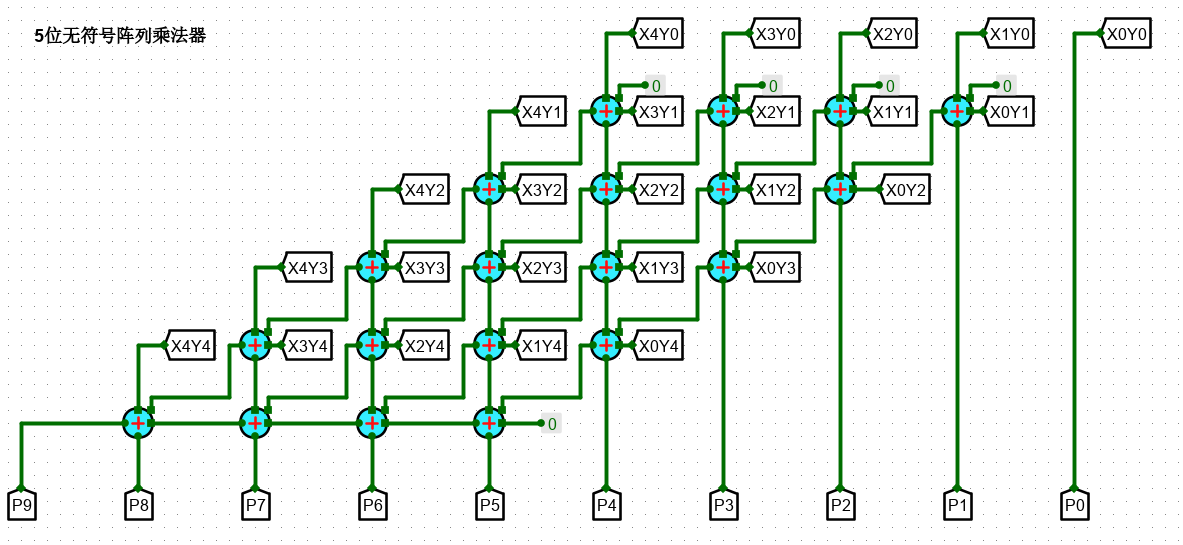
注：目前主流CPU 采用更多硬件：利用 Booth 两位乘法 + 华莱士树 的方式构建乘法器

8. 6 位补码阵列乘法器

补码想法便是利用之前的 5 位阵列乘法器。先对 乘数 进行补码（利用求补器和多路选择器），最后对结果进行再次求补后，再加上符号。

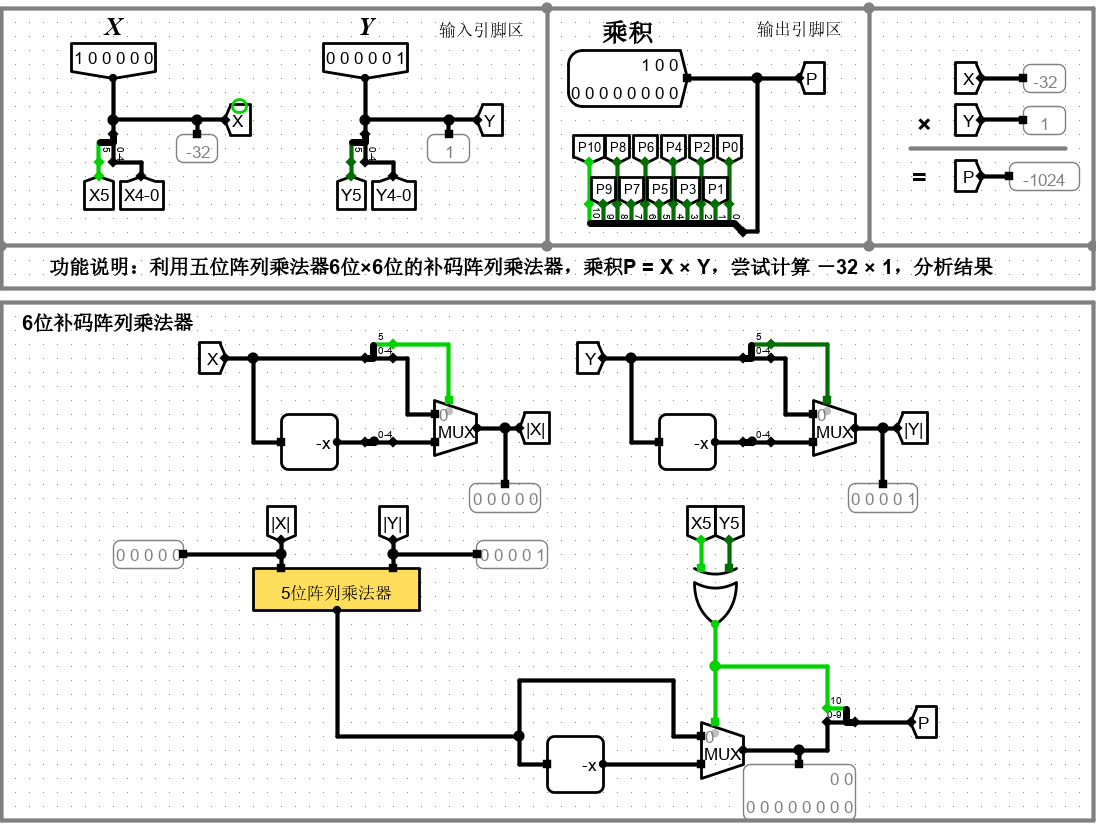
至于图中的 -32 * 1 不能得出正确结果。由探针很容易明白原因。

9. 5 位无符号乘法流水线

1.首先回忆之前的 五段流水线模拟

同步清零，气泡，高电平有效

使能端，低电平有效，stall，高电平有效

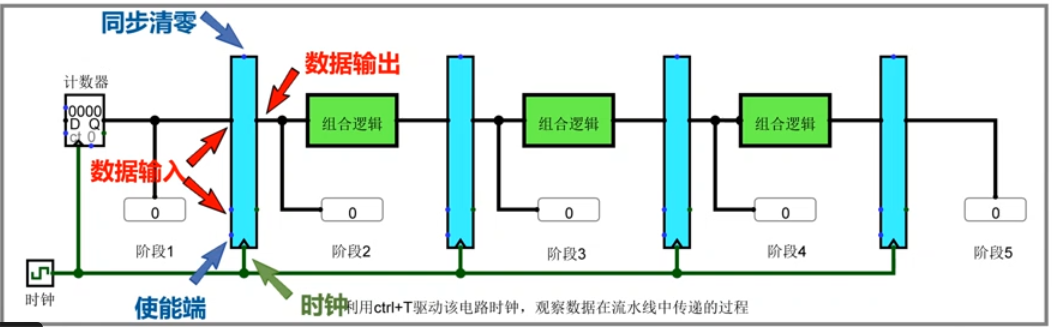
观察乘法线流水接口

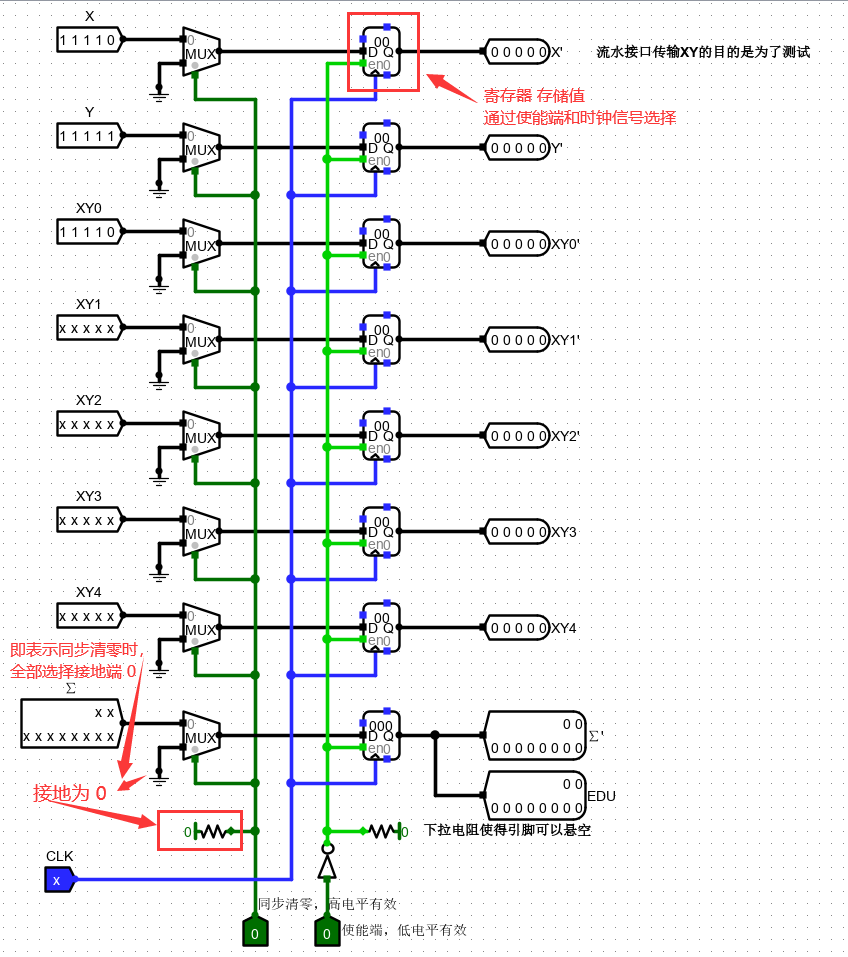
阵列乘法器流水线优化

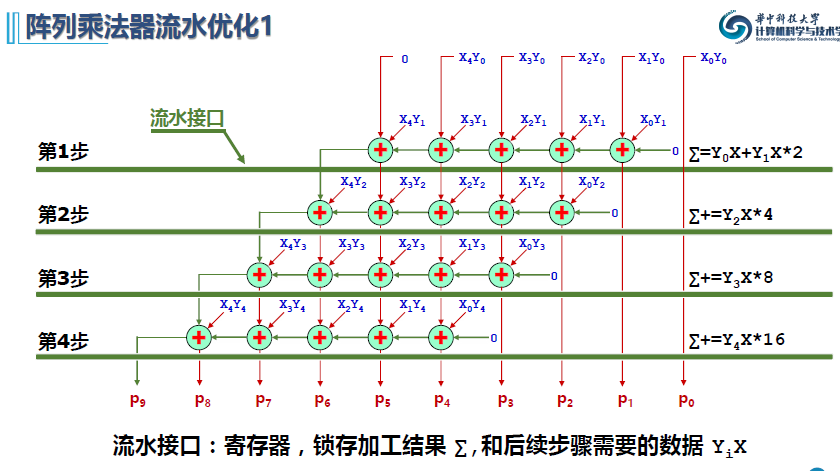
放大来看其中一个公式的实现，采用扩展器+加法器+移位器

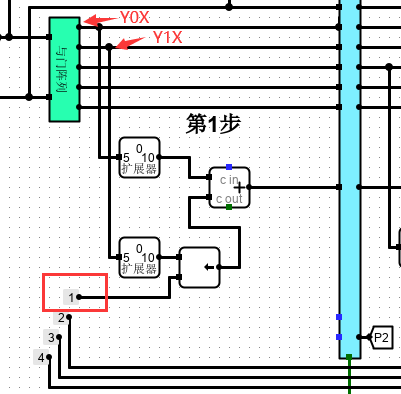
实现电路如下

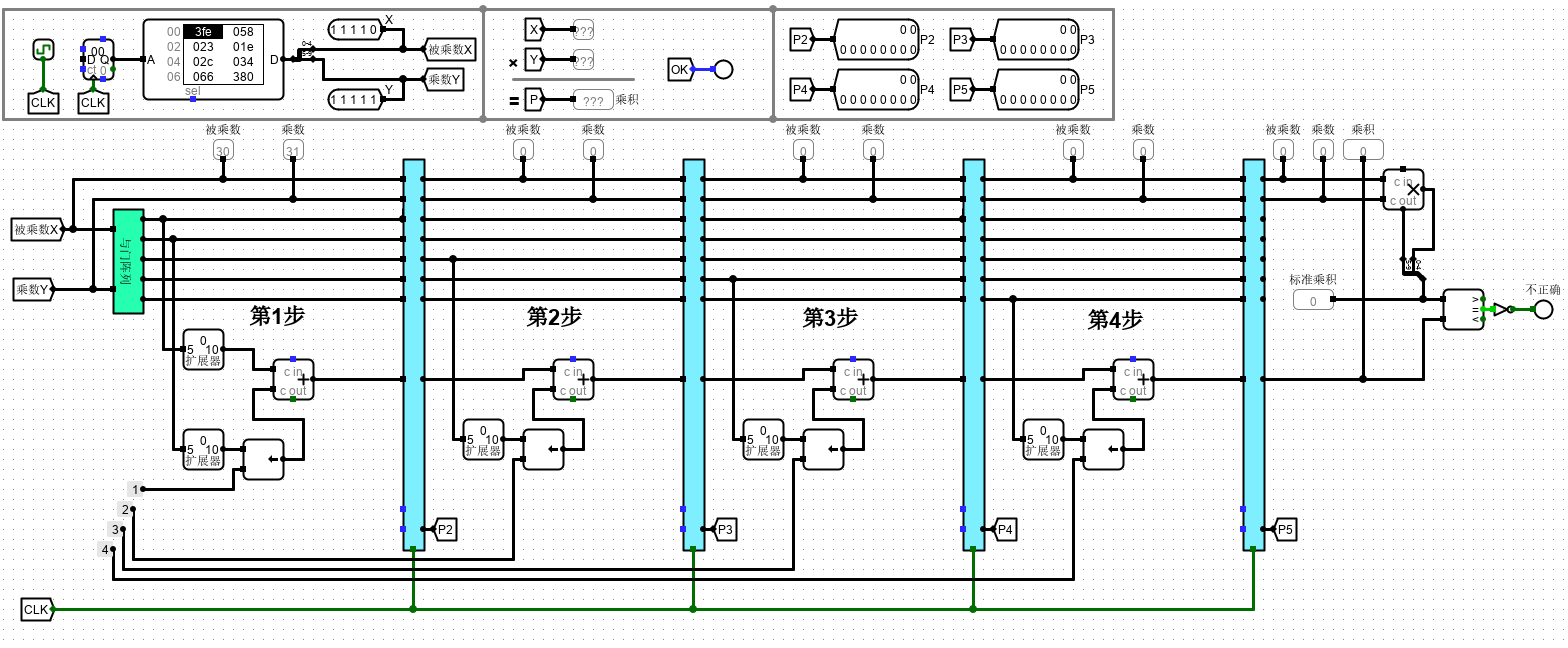
10.原码 1 位乘法器设计实验

原理

提示：无符号1位乘法自动运算可分解为如下步骤。

1. 初始化时寄存器、X、Y值全为0，电路默认状态就是0；

2. 将引脚中的两个乘数X、Y分别载入对应的寄存器，X、Y的值应送到对应寄存器的数据输入端Xa、Ya，由于寄存器的数据载入需要时钟驱动，所以在第一个时钟到来时应该将X、Y的值分别载入对应的寄存器中，此部分逻辑属于时序逻辑。

3. 计算部分积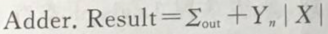其中，是寄存器乏的输出，Adder. Result 为加法器的运算结果输出，此部分核心电路是加法器，属于组合逻辑。

4. 加法器运算结果Adder.Result 逻辑右移1位送za，同时Adder.Result的最后1位加上寄存器Y的输出Yo.逻辑右移1位送 Yin，由于固定1位移位操作，所以不需要使用移位器，可直接使用Logisim平合中的分线器将对应数据分出，并且在高位补零即可实现逻辑右移，此部分逻辑属于组合逻辑。

   ​需要注意的是（即如下图），Yin 在步骤（2）中接入的是Y引脚的值，所以Ya应该增加一个多路选择器进行数据输入选择，同时引入选择控制信号，具体实现时可利用计数器的值生成该选择控制信号，当计数器初始值为0时则多路选择器选择引脚Y的值送入Yin，不为0时则选择移位数据输入。

   ​即需要注意 X Y 是分情况载入的。

   

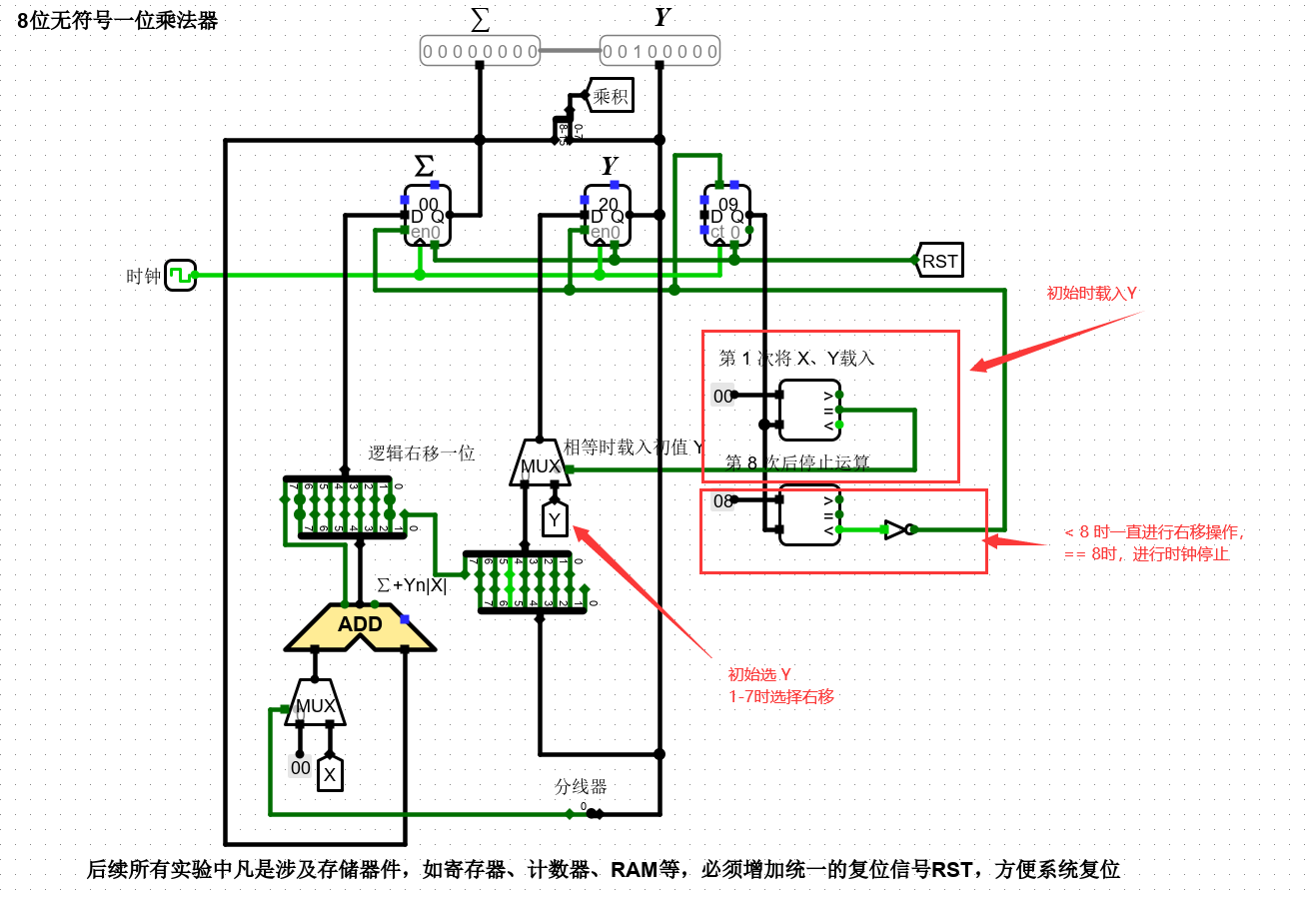
5. 将移位后的数据载入 E、Y寄存器以便进行下一次运算，载入过程受时钟控制，属时序逻辑。

6. 根据时钟计数器的值判断运算是否结束，并生成停机信号（低电平有效），停机信号应用于控制所有寄存器的使能端，使得寄存器忽略时钟输入，保持结果值不变。需要注意的是，切勿采用将时钟信号与停机信号进行逻辑与的方式控制系统停机，对时钟进行任何门级操作都会带来意想不到的潜在错误，这是后续所有实验必须遵守的原则。

移位可采用下面这种方式

需要注意的是！！！

1、下图将 E 的最后一位移入到 Y’ 中。是有下列两个原因：

1. 最后是两个寄存器保存最终 2n 长的值（类比 axdx）
2. Y’ 的移位之后，高位不影响结果，因此可以放在高部。

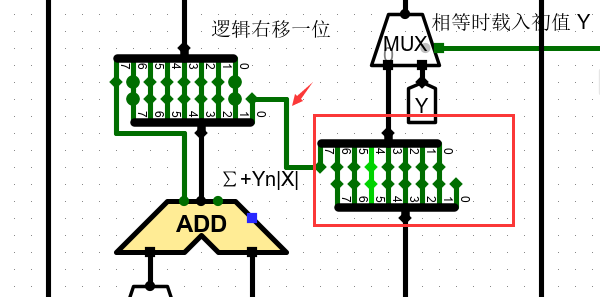
2、Y的最后一位采用分线器读入。

3、引入一个计数器，ct 连接点与寄存器大致相同。

4、停机信号应用于控制所有寄存器的使能端，使得寄存器忽略时钟输入，保持结果值不变。切勿采用将时钟信号与停机信号进行逻辑与的方式控制系统停机，对时钟进行任何门级操作都会带来意想不到的潜在错误，这是后续所有实验必须遵守的原则。

最终电路实现如下。

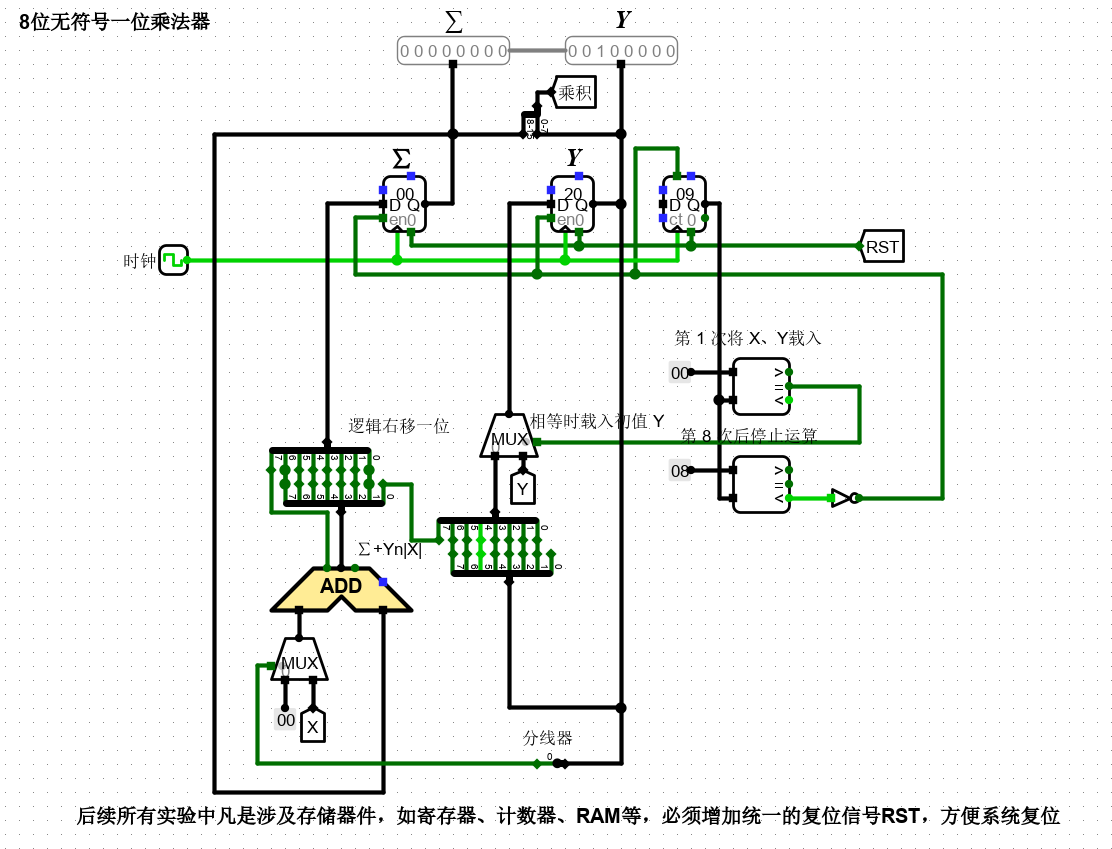
11.补码 1 位乘法器设计实验

原理的推导

首先探讨补码的一位乘

1、X 乘上 正数

由于 Y 为正，所以 [Y]补 = Y

2、X 乘上 负数

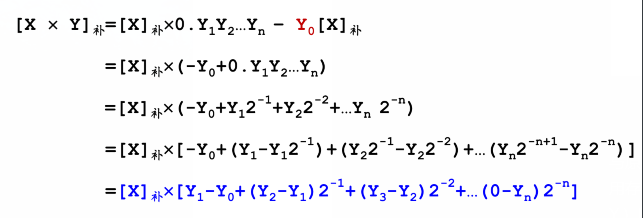
现在思考这样一个定理： 一个数向左移动一位后（2倍） – 自身 = 自身

引入一位 Yn+1，那么 Yn+1 初始值设为 0。可以得到下面式子转换。

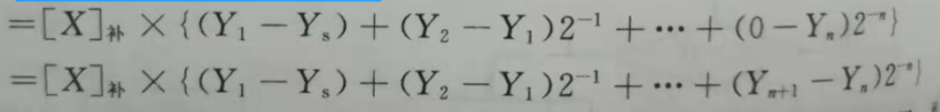
现在将 2位 看作一个整体，即 YnYn+1、Yn-1Yn、… 1 2。

即 Yn+1-Yn –> Yn 、Yn-Yn-1 –> Yn-1 …… 那么可以得到以下式子：

再由于 当 Y 为 正数 时，符号位则为 0，即可以代入下图 Y0，然后将两个情况统一。

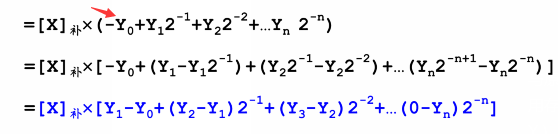
因此 这也可以解释为什么Booth里末两位为 10 时，要加[-X]补。 为什么 Y(n+1) - Yn = 1 (末两位01)的时候 要加[X]补。

易知以下推导公式（ booth 一位乘法）

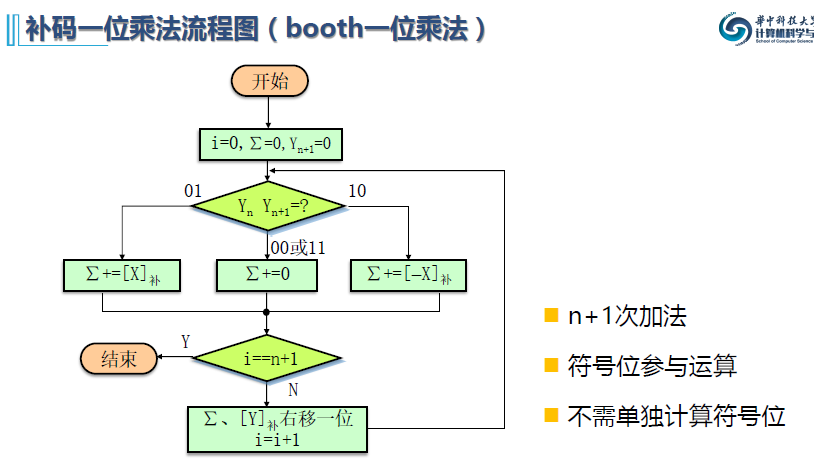
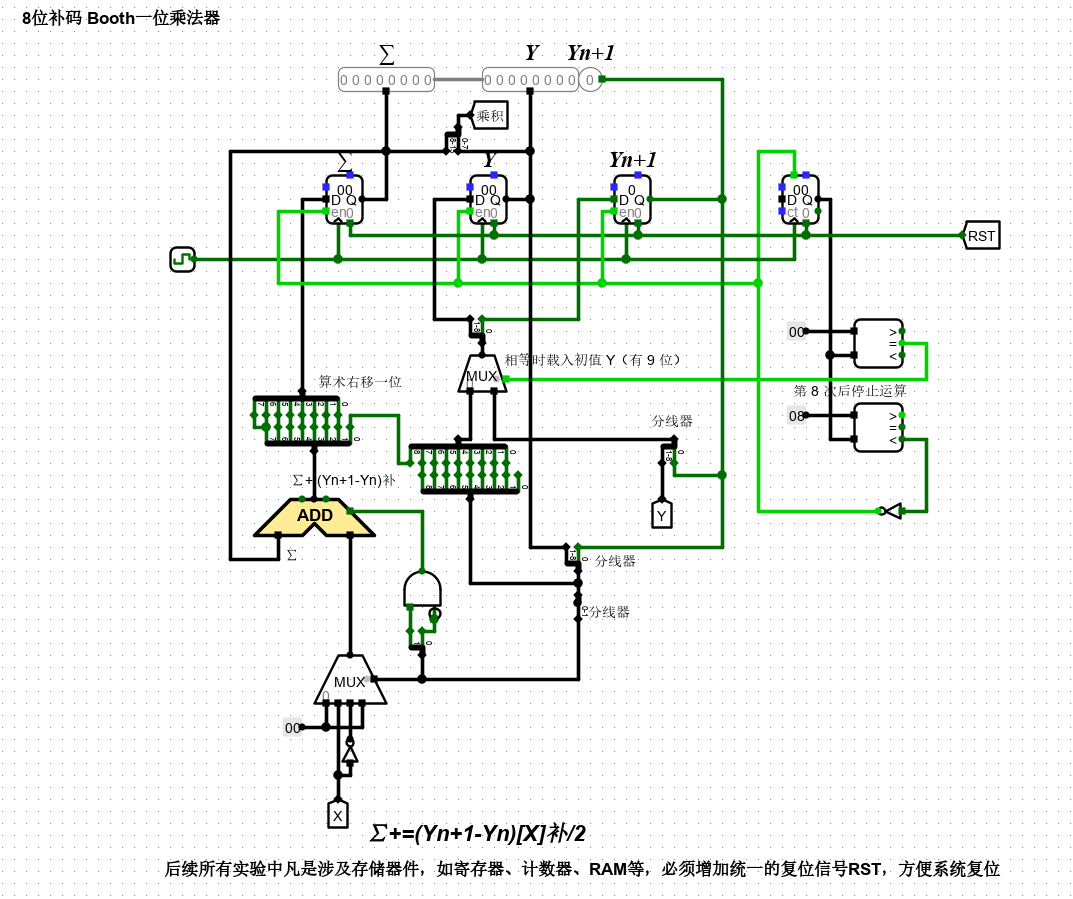
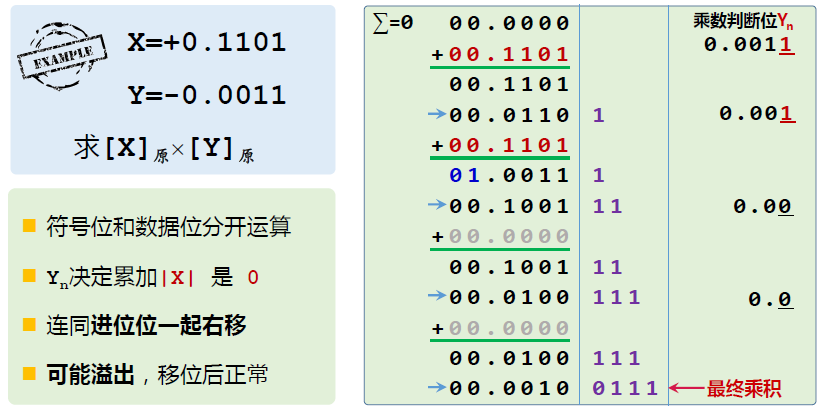
与原码1位乘法不同，booth1位乘法中乘数采用双符号位参加运算，符号位也参与运算。利用 ∑ 存放部分积，i 为循环计数器，初始值为零，部分积累加公式为 ∑ = ∑ +（Yn+1 - Yn ）[x]补，根据 Yn+1 与 Yn 的差值决定累加运算的参数是 0 还是 [X]补 或者是 [-X]补，注意最开始 Yn+1=0。运算完毕后，先判断循环次数是否达到，如未达到则部分积 ∑ 右移1位，Y 右移 1 位，然后继续循环累加，当乘数符号位参与运算后，运算结束，得到的乘积存放在 ∑ 和 Y 中，无须单独计算符号位。如果数值部分为 n 位，需要进行 n+1 次加法运算 和 n 次移位操作。

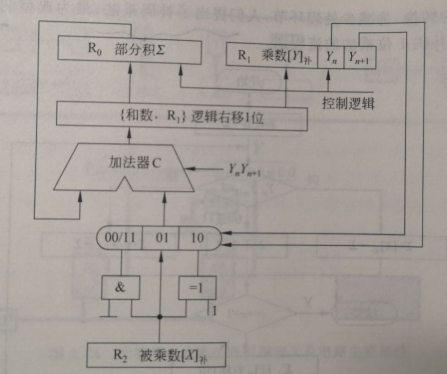
​补码1位乘法的硬件逻辑结构如上图所示，图中寄存器 R0 存放部分积 ∑ ，寄存器 R1 存放乘数 Yn 以及扩展位 Yn+1（初始值为零），YnYn+1 为判断位(最低两位)；寄存器R2：存放被乘数X的补码；加法器实现部分积的累加，运算逻辑为

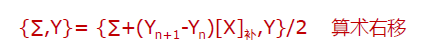
其中，一个操作数为 ∑ ，另一个操作数由判断位 YnYn+1 对多路选择器进行选择控制； 控制电路负责移位控制和循环计数。受时钟驱动，每运算一次，加法器运算结果与寄存器 R1 的值一起算术右移 1 位后产生的新值载入 R0 和 R1 寄存器中，当运算结束时，乘积的高 n 位数据在 R0 中，低 n 位在 R1 中， R1 中原来的乘数在右移过程中逐位移出寄存器。

• 乘数 x 取双符号位参与运算，部分积的初始值为0；
• 乘数 y 取单符号位参与运算。

注意事项如下：

1、Yn+1 初始值为 0 。

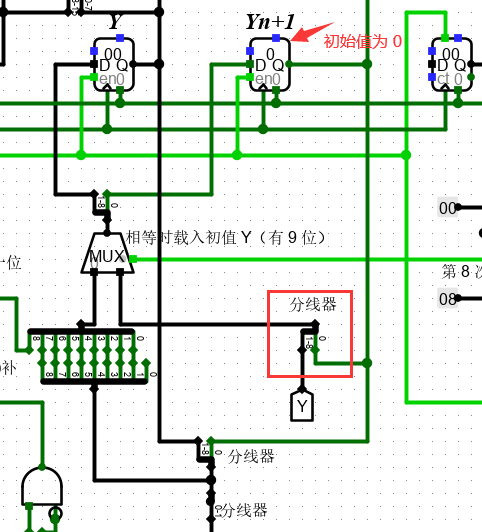
2、最高位与次高位一致

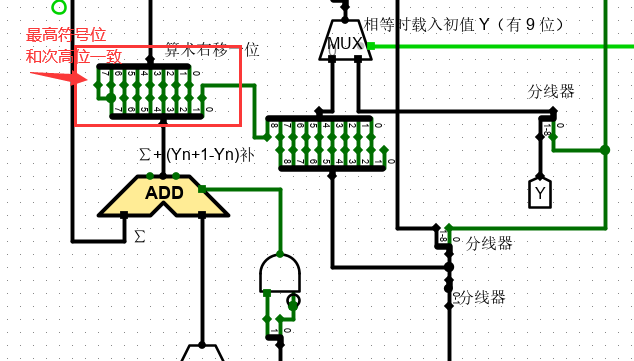
3、负数取补 = 取反 + 1

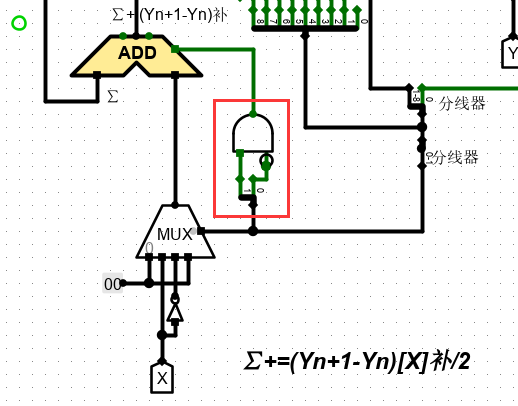
最终电路实现如下：（思路大致与原码 1 位一样）